Stoffer's GitHome

GitHome Little Dogies

View on GitHub

R Tutorial

Appendectomy: This site replaces Appendix R in the texts Time Series Analysis and Its Applications: With R Examples and Time Series: A Data Analysis Approach Using R both by Shumway & Stoffer

🔸 🔸 🔸 🔸 🔸

Table of Contents


Installing R

R is an open source statistical computing and graphics system that runs on many operating systems. It comes with a very minimal GUI (except for Linux) with which a user can type a command, press enter, and an answer is returned. In Linux, it runs in a terminal.

🐒 To obtain R, point your browser to the Comprehensive R Archive Network (CRAN) and download and install it. The installation includes help files and some user manuals. An internet search can pull up various short tutorials and videos, for example, R Cookbook, Hands-On Programming with R and the website Quick-R. And we state the obvious:

    If you can’t figure out how to do something, do an internet search.

🔸 🔸 🔸 🔸 🔸

sudo snap install notepad-plus-plus

Sorry, no notepad++ for Mac or Cheese 🍲.

🔸 🔸 🔸 🔸 🔸


There are some simple exercises that will help you get used to using R. For example,


top


Packages and ASTSA

At this point, you should have R up and running.

❓ Ready …

The capabilities of R are extended through packages. R comes with a number of preloaded packages that are available immediately.

Most packages can be obtained from CRAN and its mirrors. The package used extensively in the text is astsa (Applied Statistical Time Series Analysis). Get it now:

The latest version of astsa will always be available from GitHub. More information may be found at ASTSA NEWS.

Except for base packages, to use a package you have to load it after starting R, for example:

library(astsa)

You may want to create a .First function as follows,

.First <- function(){library(astsa)}

and save the workspace when you quit, then astsa will be loaded at every start. Other startup commands can be added later.

We will use the xts package and the zoo package throughout the text. To install both, start R and type

install.packages("xts")  # installs both xts and zoo

And again, to use the package you must load it first by issuing the command

library(xts)

This is a good time to get those packages:


🔸🔸🔸🔸🔸🔸🔸

⛔ ⛔ WARNING: If loaded, the package dplyr may (and most likely will) corrupt the base scripts filter and lag from the stats package that we use often. In this case, to avoid problems when analyzing time series, here are some options:

(1) # either detach it
detach(package:dplyr)  

(2) # or fix it yourself if you want dplyr
# this is a great idea from  https://stackoverflow.com/a/65186251
library(dplyr, exclude = c("filter", "lag"))  # remove the culprits
Lag <- dplyr::lag            # and do what the dplyr ... 
Filter <- dplyr::filter      # ... maintainer refuses to do
# and then use Lag and Filter for the corresponding dplyr commands

(3) # or just take back the commands 
filter = stats::filter
lag = stats::lag

 # in this case, you can still use these for dplyr
 Lag <- dplyr::lag     
 Filter <- dplyr::filter

😖 If you are wondering how it is possible to corrupt a base package, 👽 you are not alone.

🔸🔸🔸🔸🔸🔸🔸


Getting Help

R is not consistent with help files across different operating systems. The R html help system can be started by issuing the command

help.start()

The help files for installed packages can also be found there. Notice the parentheses in the commands above; they are necessary to run scripts. If you simply type

help.start

nothing will happen and you will just see the commands that make up the script. To get help for a particular command, say library, do this:

help(library) 
?library        # same thing

Notice the use of a semicolon for multiple commands on one line.


❌ After viewing enough help files, you will eventually run into ## Not run: in an Examples section. Why would an example be given with a warning NOT to run it?

Not run just tells CRAN not to check the example for various reasons such as it takes a long time to run … it sort of runs against the idea that help files should be helpful or at least not make things worse. Bottom line: Ignore it. It is NOT for a user's consumption. If you are using html help and you see this, then Run Examples will not do anything. In this case, you just copy-and-paste the code to run it.


Finally, you can find lots of help on the internet 🤔. If you have a specific and difficult question, try Stack Overflow.


top


Basics

The convention throughout the texts is that R code is in blue with red operators, output is purple , and comments are green. This does not apply to this site where syntax highlighting is controlled by your browser and GitHub.

Get comfortable, start R and try some simple tasks.

2+2           # addition 
 [1] 5

5*5 + 2       # multiplication and addition 
 [1] 27

5/5 - 3       # division and subtraction 
 [1] -2

log(exp(pi))  # log, exponential, pi 
 [1] 3.141593

sin(pi/2)     # sinusoids
 [1] 1

2^(-2)        # power
 [1] 0.25 

sqrt(8)       # square root
 [1] 2.828427

-1:5           # sequences
 [1] -1  0  1  2  3  4  5

seq(1, 10, by=2)   # sequences 
 [1] 1 3 5 7 9

rep(2, 3)     # repeat 2 three times
 [1] 2 2 2
  
6/2*(1+2)     # not one
 [1] 9  

 [1] 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 0.0
[11] 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 0.0

Let’s get complex:

1/1i  
 [1] 0-1i    # complex numbers are displayed as a+bi

🎀 Extra credit: $e^{i \pi} + 1 =0$ is a famous formula that uses the five most basic values in mathematics. Whose name is associated with this awesome equation?

Ok, now try this.


top


Objects and Assignment

Next, we’ll use assignment to make some objects:

x <- 1 + 2  # put 1 + 2 in object x

x = 1 + 2   # same as above with fewer keystrokes

1 + 2 -> x  # same

x           # view object x
 [1]  3

(y = 9 * 3)   # put 9 times 3 in y and view the result 
 [1] 27

(z = rnorm(5))  # put 5 standard normals into z and print z
 [1]  0.96607946  1.98135811 -0.06064527  0.31028473  0.02046853

Vectors can be of various types, and they can be put together using c() [concatenate or combine]; for example

x <- c(1, 2, 3)             # numeric vector

y <- c("one","two","three") # character vector

z <- c(TRUE, TRUE, FALSE)   # logical vector

Missing values are represented by the symbol NA, $\infty$ by Inf and impossible values are NaN (not a number). Here are some examples:

( x = c(0, 1, NA) )
 [1]  0  1 NA  

2*x
 [1]  0  2 NA  

is.na(x)
 [1] FALSE FALSE  TRUE  

x/0 
 [1] NaN Inf  NA

There is a difference between <- and =. From R help(assignOps), you will find: The operator <- can be used anywhere, whereas the operator = is only allowed at the top level … .

x = 0 = y
x <- 0 -> y


Here’s a thing about TRUE and FALSE 🤔. T and F are initially set to TRUE and FALSE, so this works if you want object AmInice to be TRUE:

AmInice = T
AmInice
 [1] TRUE

But this is bad practice because it can be easily wrecked, for example, if you set T to something else and then later …. :

T = 17
AmInice = T
AmInice 
 [1] 17

Bottom line, get used to using the whole words TRUE and FALSE and don’t use the T and F shortcuts. This is especially concerning because T and F are some of our favorite distributions.


🔸🔸🔸🔸🔸

♻ It is worth pointing out R’s recycling rule for doing arithmetic. Note again the use of the semicolon for multiple commands on one line.

x = c(1, 2, 3, 4); y = c(2, 4); z = c(8, 3, 2)

x * y    
 [1]  2  8  6 16 

y + z    # oops
 [1] 10  7  4 
 Warning message:
 In y + z : longer object length is not a multiple of shorter object length

The following commands are useful:

ls()                # list all objects
 "dummy" "mydata" "x" "y" "z"

ls(pattern = "my")  # list every object that contains "my" 
 "dummy" "mydata"

rm(dummy)           # remove object "dummy"

rm(list=ls())       # remove almost everything (use with caution)

data()              # list of available data sets

help(ls)            # specific help (?ls is the same)

getwd()             # get working directory

setwd()             # change working directory

q()                 # end the session (keep reading)

and a reference card may be found here.

🔸🔸🔸🔸🔸

✨ When you quit, R will prompt you to save an image of your current workspace. Answering yes will save the work you have done so far, and load it when you next start R. We have never regretted selecting yes, but we have regretted answering no.

If you want to keep your files separated for different projects, then having to set the working directory each time you run R is a pain. If you use RStudio, then you can easily create separate projects. There are some easy work-arounds, but it depends on your OS. In Windows, copy the R shortcut into the directory you want to use for your project. Right click on the shortcut icon, select Properties, and remove the text in the Start in: field; leave it blank and press OK. Then start R from that shortcut (works for RStudio too).

library(astsa)
help(cpg)     # or ?cpg
 #  Median annual cost per gigabyte (GB) of storage. 
write(cpg, file="cpg.txt", ncolumns=1)   

getwd()
 [1] "/home/TimeSeries"

Now find the file and look at it… there should be 29 numbers in one column.

To create your own data set, you can make a data vector as follows:

mydata = c(1,2,3,2,1)

Now you have an object called mydata that contains five elements. R calls these objects vectors even though they have no dimensions (no rows, no columns); they do have order and length:

mydata         # display the data 
 [1] 1 2 3 2 1

mydata[3:5]    # elements three through five 
 [1] 3 2 1

mydata[-(1:2)] # everything except the first two elements
 [1] 3 2 1

length(mydata) # number of elements
 [1] 5

scale(mydata)  # standardize the vector of observations
            [,1]
 [1,] -0.9561829
 [2,]  0.2390457
 [3,]  1.4342743
 [4,]  0.2390457
 [5,] -0.9561829
 attr(,"scaled:center")
 [1] 1.8
 attr(,"scaled:scale")
 [1] 0.83666 

dim(mydata)    # no dimensions
 NULL

mydata = as.matrix(mydata)  # make it a matrix

dim(mydata)    # now it has dimensions
 [1] 5 1

🔸🔸🔸🔸🔸

If you have an external data set, you can use scan or read.table (or some variant) to input the data. For example, suppose you have an ascii (text) data file called dummy.txt in your working directory, and the file looks like this:

-----------
1 2 3 2 1
9 0 2 1 0
-----------

(dummy = scan("dummy.txt") )        # scan and view it
 Read 10 items
  [1] 1 2 3 2 1 9 0 2 1 0

(dummy = read.table("dummy.txt") )  # read and view it 
 V1 V2 V3 V4 V5
  1  2  3  2  1
  9  0  2  1  0

There is a difference between scan and read.table. The former produced a data vector of 10 items while the latter produced a data frame with names V1 to V5 and two observations per variate.

(cost_per_gig = scan("cpg.txt") )  # read and view
  Read 29 items
  [1] 2.13e+05 2.95e+05 2.60e+05 1.75e+05 1.60e+05
  [6] 7.10e+04 6.00e+04 3.00e+04 3.60e+04 9.00e+03 
 [11] 7.00e+03 4.00e+03 ...

When you use read.table or similar, you create a data frame. In this case, if you want to list (or use) the second variate, V2, you could use

dummy$V2
 [1] 2 0

and so on. You might want to look at the help files ?scan and ?read.table now. Data frames (?data.frame) are used as the fundamental data structure by most of R’s modeling software. Notice that R gave the columns of dummy generic names, V1,..., V5. You can provide your own names and then use the names to access the data without the use of $ as above.

colnames(dummy) = c("Dog", "Cat", "Rat", "Pig", "Man")

attach(dummy)    # this can cause problems; see ?attach

Cat              # view the vector Cat
  [1] 2 0 

Rat*(Pig - Man)  # animal arithmetic  
  [1] 3 2 

head(dummy)      # view the first few lines of a data file

detach(dummy)    # clean up

R is case sensitive, thus cat and Cat are different. Also, cat is a reserved name (?cat), so using cat instead of Cat may cause problems later. It is noted that attach can lead to problems: The possibilities for creating errors when using attach are numerous. Avoid. If you use it, it is best to clean it up when you are done.

You can also use save and load to work with R compressed data files if you have large files. If interested, investigate the use of the save and load commands. The best way to do this is to do an internet search on R save and load, but you knew this already.

You may also include a header in the data file to avoid colnames. For example, if you have a comma separated values file dummy.csv that looks like this,

--------------------------
Dog, Cat, Rat, Pig, Man
1, 2, 3, 2, 1
9, 0, 2, 1, 0
--------------------------

then use the following command to read the data.

(dummy = read.csv("dummy.csv")) 
     Dog Cat Rat Pig Man
   1   1   2   3   2   1
   2   9   0   2   1   0

The default for .csv files is header=TRUE, type ?read.table for further information on similar types of files.

Two commands that are used frequently to manipulate data are cbind for column binding and rbind for row binding. The following is an example.

options(digits=2)  # significant digits to print - default is 7

x = runif(4)       # generate 4 values from uniform(0,1) into object x

y = runif(4)       # generate 4 more and put them into object y

cbind(x,y)         # column bind the two vectors (4 by 2 matrix) 
          x    y
  [1,] 0.90 0.72
  [2,] 0.71 0.34
  [3,] 0.94 0.90
  [4,] 0.55 0.95

rbind(x,y)         # row bind the two vectors (2 by 4 matrix)
    [,1] [,2] [,3] [,4]
  x 0.90 0.71 0.94 0.55
  y 0.72 0.34 0.90 0.95

a = seq(1, 10, by=2)

b = seq(2, 10, by=2)

x = cbind(a, b)

x[,1]
 [1] 1 3 5 7 9 

x[,2]
 [1]  2  4  6  8 10

Summary statistics of a data set are fairly easy to obtain. We will simulate 25 normals with $\mu=10$ and $\sigma=4$ and then perform some basic analyses. The first line of the code is set.seed, which fixes the seed for the generation of pseudorandom numbers. Using the same seed yields the same results; to expect anything else would be insanity.

options(digits=3)       # output control 

set.seed(911)           # so you can reproduce these results

x = rnorm(25, 10, 4)    # generate the data

summary(x)
  Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  4.46    7.58   11.47   11.35   13.69   21.36 

c( mean(x), median(x), var(x), sd(x) )  # guess
 [1] 11.35 11.47 19.07  4.37

c( min(x), max(x) )     # smallest and largest values
 [1] 4.46 21.36 

which.max(x)            # index of the max (x[20] in this case) 
 [1] 20 

boxplot(x);  hist(x);  stem(x)   # visual summaries (not shown)

set.seed(911)        # you can cheat -or-
boxplot(rnorm(100))  # reissue until you see at least 2 outliers

🍉 Extra Credit: When is an outlier not an outlier? Answer forthcoming.

🔸🔸🔸🔸🔸

It can’t hurt to learn a little about programming in R because you will see some of it along the way. First, let’s try a simple example of a function that returns the reciprocal of a number:

oneover <- function(x){ 1/x }

oneover(0)
 [1] Inf 

oneover(-4)
 [1] -0.25

A script can have multiple inputs, for example, guess what this does:

xtimesy <- function(x,y){ x * y }    
xtimesy(20, .5)  # and try it
  [1] 10 

pwr <- function(x, y){ x^y }
pwr(25, .5)
  [1] 5

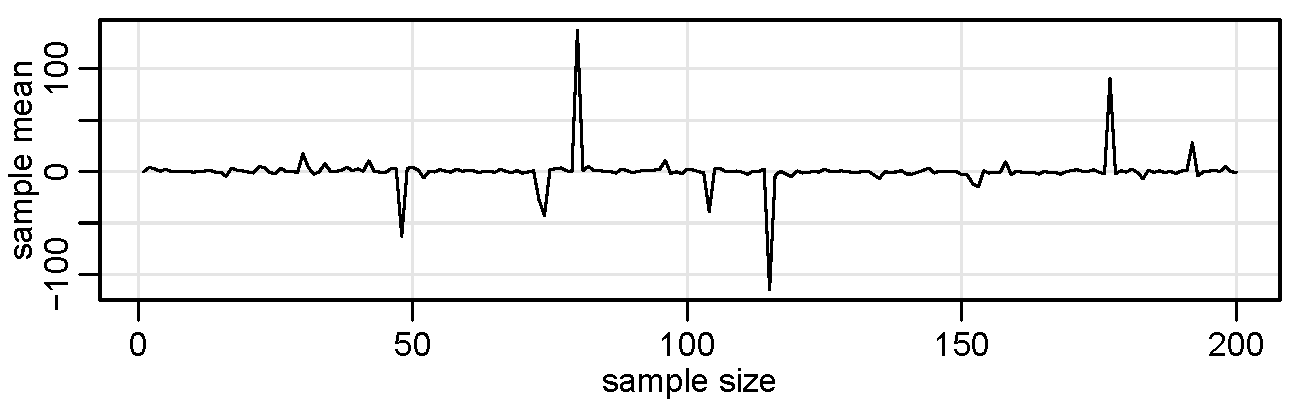
Finally, consider a simple program that we will call crazy to produce a graph of a sequence of sample means of increasing sample sizes from a Cauchy distribution with location parameter zero.

crazy <- function(num) {   # start the script - 1 argument, num, is final sample size
  x <- c()                 # start a vector in object x
  for (n in 1:num) { x[n] <- mean(rcauchy(n)) }  # x[n] holds mean of n standard Cauchys
  plot(x, type="l", xlab="sample size", ylab="sample mean") # plot mean for each sample size n
  }                        # end/close the script

set.seed(1001)   # set a seed (not necessary) and
crazy(200)       # run it - plot below

crazy


top


Regression and Time Series Primer

These topics run throughout the text, but we will give a brief introduction here. The workhorse for linear regression in R is lm(). Suppose we want to fit a simple linear regression, $y = \alpha + \beta x + \epsilon$. In R, the formula is written as y~x. Let’s simulate some data and do a simple example first.

set.seed(666)           # not that 666       

x = rnorm(10)           # generate 10 standard normals  

y = 1 + 2*x + rnorm(10) # generate a simple linear model

summary(fit <- lm(y~x)) # fit the model - summarize results
   Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
  (Intercept)   1.0680     0.3741   2.855 0.021315    
  x             1.6778     0.2651   6.330 0.000225  
  ---
  Residual standard error: 1.18 on 8 degrees of freedom
  Multiple R-squared:  0.8336,    Adjusted R-squared:  0.8128 
  F-statistic: 40.07 on 1 and 8 DF,  p-value: 0.0002254

plot(x, y)              # scatterplot of data (see below)

abline(fit, col=4)      # add fitted blue line (col 4) to the plot

Note that we put the results into an object we called fit; this object contains all of the information about the regression. Then we used summary to display some of the results and used abline to plot the fitted line. The command abline is useful for drawing horizontal and vertical lines also.

abline(v=mean(x), h=mean(y), col=2, lty=2)  # col 2 is red and lty 2 is dashed

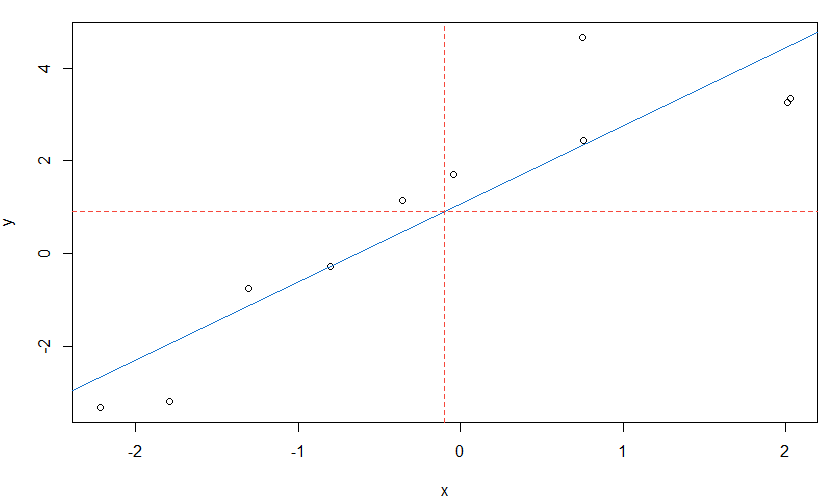
lmplot


The lm object that we called fit in our simulation contains all sorts of information that can be extracted. Sometimes, however, it might be difficult to find where that information is stored. The easiest way to find what is stored in an object is to look at the structure of the object. We list only a partial output because this particular list is very long.

str(fit)     # partial listing below
  List of 12
   $ coefficients : Named num [1:2] 1.07 1.68
    ..- attr(*, "names")= chr [1:2] "(Intercept)" "x"
   $ residuals    : Named num [1:10] 2.325 -1.189 0.682 -1.135 -0.648 ...
    ..- attr(*, "names")= chr [1:10] "1" "2" "3" "4" ...
   $ fitted.values: Named num [1:10] 2.332 4.448 0.472 4.471 -2.651 ...
    ..- attr(*, "names")= chr [1:10] "1" "2" "3" "4" ...

For example, the parameter estimates are in fit$coef or coef(fit). We can get the residuals from fit$resid or resid(fit) and the commands fit$fitted or fitted(fit) will display the fitted values. For example, we may be interested in plotting the residuals in order or in plotting the residuals against the fitted values:

plot(resid(fit))              # not shown

plot(fitted(fit), resid(fit)) # not shown

🔸🔸🔸🔸🔸

Time Series

Let’s focus a little on time series. To create a time series object, use the command ts. Related commands are as.ts to coerce an object to a time series and is.ts to test whether an object is a time series. First, make a small data set:

(mydata = c(1,2,3,2,1) ) # make it and view it
  [1] 1 2 3 2 1

Make it an annual time series that starts in 2020:

(mydata = ts(mydata, start=2020) )
  Time Series:
  Start = 2020
  End = 2024
  Frequency = 1
  [1] 1 2 3 2 1

Now make it a quarterly time series that starts in 2020-III:

(mydata = ts(mydata, start=c(2020,3), frequency=4) )
       Qtr1 Qtr2 Qtr3 Qtr4
  2020              1    2
  2021    3    2    1     

time(mydata)  # view the dates  
          Qtr1    Qtr2    Qtr3    Qtr4 
  2020                 2020.50 2020.75
  2021 2021.00 2021.25 2021.50

To use part of a time series object, use window():

( x = window(mydata, start=c(2021,1), end=c(2021,3)) )
       Qtr1 Qtr2 Qtr3
  2021    3    2    1

Next, we’ll look at lagging and differencing, which are fundamental transformations used frequently in the analysis of time series. For example, if I’m interested in predicting todays from yesterdays, I would look at the relationship between $x_t$ and its lag, $x_{t-1}$.

Now let’s make a simple series $x_t$

x = ts(1:5)

Then, column bind (cbind) lagged values of $x_t$ and you will notice that lag(x) is forward lag, whereas lag(x, -1) is backward lag.

cbind(x, lag(x), lag(x,-1))
       x   lag(x)   lag(x, -1)
  0   NA      1        NA
  1    1      2        NA
  2    2      3         1
  3    3      4         2  <- # in this row, for example, x is 3, 
  4    4      5         3     #  lag(x) is ahead at 4, and  
  5    5     NA         4     #   lag(x,-1) is behind at 2  
  6   NA     NA         5

Compare cbind and ts.intersect:

ts.intersect(x, lag(x,1), lag(x,-1)) 
  Time Series:  Start = 2  End = 4  Frequency = 1
      x   lag(x, 1)   lag(x, -1)
  2   2         3          1
  3   3         4          2
  4   4         5          3

🏮 When using lagged values of various series, it is usually necessary to use ts.intersect to align them by time. You will see this play out as you work through the text.

To examine the time series attributes of an object, use tsp. For example, one of the time series in astsa is the US unemployment rate:

tsp(UnempRate)
 [1] 1948.000 2016.833   12.000
#    start    end        frequency

which starts January 1948, ends in November 2016 (10/12 &approx; .833), and is monthly data (frequency = 12).

For discrete-time series, finite differences are used like differentials. To difference a series, $\nabla x_t = x_t - x_{t-1}$, use

diff(x)

but note that

diff(x, 2)

is $x_t - x_{t-2}$ and not second order differencing. For second-order differencing, that is, $\nabla^2 x_t = \nabla (\nabla x_t)$, do one of these:

diff(diff(x))

diff(x, diff=2)   # same thing

and so on for higher-order differencing.

💲 You have to be careful if you use lm() for lagged values of a time series. If you use lm(), then what you have to do is align the series using ts.intersect. Please read the warning Using time series in the lm() help file [help(lm)]. Here is an example regressing astsa data, weekly cardiovascular mortality ($M_t$ cmort) on particulate pollution ($P_t$ part) at the present value and lagged four weeks ($P_{t-4}$ part4). The model is

\[M_t = \alpha + \beta_1 P_t + \beta_2 P_{t-4} + w_t\,,\]

where we assume $w_t$ is the usual normal regression error term. First, we create the data matrix ded, which consists of the intersection of the three series:

library(astsa)   # load astsa first

ded = ts.intersect(cmort, part, part4=lag(part,-4))

Now the series are all aligned and the regression will work.

summary(fit <- lm(cmort ~ part + part4, data = ded, na.action = NULL) )
  Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
  (Intercept) 69.01020    1.37498  50.190  < 2e-16  
  part         0.15140    0.02898   5.225 2.56e-07  
  part4        0.26297    0.02899   9.071  < 2e-16  
  ---
  Residual standard error: 8.323 on 501 degrees of freedom
  Multiple R-squared:  0.3091,    Adjusted R-squared:  0.3063 
  F-statistic: 112.1 on 2 and 501 DF,  p-value: < 2.2e-16

There was no need to rename lag(part,-4) to part4, it’s just an example of what you can do. Also, na.action=NULL is necessary to retain the time series attributes. It should be there whenever you do time series regression.

part4 <- lag(part, -4)

summary(fit <- lm(cmort~ part + part4, na.action=NULL) )
  Coefficients: (1 not defined because of singularities) # OUCH!
               Estimate Std. Error t value Pr(>|t|)    
   (Intercept) 74.79860    1.30943   57.12   <2e-16 
   part         0.29317    0.02631   11.14   <2e-16 
   part4             NA         NA      NA       NA

An alternative to the above is the package dynlm, which has to be installed. After the package is installed, you can do the previous example as follows:

library(dynlm)                           # load the package

fit = dynlm(cmort ~ part + L(part,4))    # ts.intersect not needed

summary(fit)
  Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
  (Intercept) 69.01020    1.37498  50.190  < 2e-16 
  part         0.15140    0.02898   5.225 2.56e-07 
  L(part, 4)   0.26297    0.02899   9.071  < 2e-16 
  ---
  Residual standard error: 8.323 on 501 degrees of freedom 
  Multiple R-squared:  0.3091,    Adjusted R-squared:  0.3063 
  F-statistic: 112.1 on 2 and 501 DF,  p-value: < 2.2e-16

In Chapter 1 problems, you are asked to fit a regression model \(x_t = \beta t + \alpha_1 Q_1(t) + \alpha_2 Q_2(t) + \alpha_3 Q_3(t) + \alpha_4 Q_4(t) + w_t\) where $x_t$ is logged Johnson & Johnson quarterly earnings ($n=84$), and $Q_i(t)$ is the indicator of quarter $i=1,2,3,4$. The indicators can be made using factor.

trend = time(jj) - 1970        # helps to 'center' time
Q     = factor(cycle(jj))      # make (Q)uarter factors
reg   = lm(log(jj) ~ 0 + trend + Q, na.action = NULL)  # 0 = no intercept

summary(reg)                   # view the results (not shown)

model.matrix(reg)              # view the model design matrix
          trend Q1 Q2 Q3 Q4
     1  -10.00  1  0  0  0
     2   -9.75  0  1  0  0
     3   -9.50  0  0  1  0
     4   -9.25  0  0  0  1
     5   -9.00  1  0  0  0
     .     .    .  .  .  .
     .     .    .  .  .  .

We’ll end this part with simulating ARIMA models. If you don’t know what that means then it’s ok, you will by the time you finish the course, and you can skip ahead or do something else now.

🐎 The workhorse for ARIMA simulations is sarima.sim from astsa. Here are some examples; no output is shown so you’re on your own. Note that tsplot is the generic astsa script for plotting time series. Graphics is the next subject.

library(astsa)  # load astsa

## AR(2) with mean 50 [n = 500 is default]
y = sarima.sim(ar=c(1.5,-.75)) + 50
tsplot(y)

## ARIMA(0,1,1) with drift ['mean' refers to the innovations] 
tsplot(sarima.sim(ma=-.8, d=1, mean=.1))

## SAR(1) example from text
set.seed(666)   # not that 666
sAR = sarima.sim(sar=.9, S=12, n=36)
tsplot(sAR, type='c')
points(sAR, pch=Months, cex=1.1, font=4, col=1:4)

## SARIMA(0,1,1)x(0,1,1)_12 - B&J's favorite
set.seed(101010)
tsplot(sarima.sim(d=1, ma=-.4, D=1, sma=-.6, S=12, n=120))  

## infinite variance t-errors 
tsplot(sarima.sim(ar=.9, rand.gen=function(n, ...) rt(n, df=2) ))

## use your own innovations
dog = rexp(150, rate=.5)*sign(runif(150,-1,1))
tsplot(sarima.sim(n=100, ar=.99, innov=dog, burnin=50))

## generate seasonal data but no P, D or Q - you will receive 
## a message to make sure that you wanted to do this on purpose: 
tsplot(sarima.sim(ar=c(1.5,-.75), n=144, S=12), ylab='doggy', xaxt='n')
mtext(seq(0,144,12), side=1, line=.5, at=0:12)


top


Graphics


R Time Series Issues


More on ASTSA


R Code in Texts

top













🐒 𝔼 ℕ 𝔻 🐒